The Lambda Cold Dark Matter (ΛCDM) model, also known as the Lambda Cold Dark Matter cosmological model, is the prevailing framework in cosmology for explaining the large-scale structure and evolution of the universe. It combines the effects of dark energy, dark matter, and ordinary matter to provide a comprehensive description of the universe’s composition and dynamics. Here’s a detailed breakdown of the ΛCDM model
1. Components of the ΛCDM Model
a. Lambda (Λ) – Dark Energy:
- Cosmological Constant (Λ): The term Λ represents the cosmological constant, a form of dark energy with a constant energy density throughout space. It was originally introduced by Einstein in 1917 to allow for a static universe but was later discarded. It gained renewed importance with the discovery of accelerated cosmic expansion.
- Role: Dark energy (Λ) drives the accelerated expansion of the universe. It counteracts the gravitational attraction of matter and dark matter, leading to the observed acceleration in the rate of expansion.
b. Cold Dark Matter (CDM):
- Nature: Cold dark matter refers to dark matter that moves slowly compared to the speed of light and does not interact electromagnetically, meaning it does not emit, absorb, or reflect light. It is “cold” because it is non-relativistic and thus clumps together more readily under the influence of gravity.
- Role: CDM helps explain the formation of large-scale structures in the universe, such as galaxies and clusters of galaxies. Its gravitational effects play a crucial role in the structure formation and distribution of visible matter.
c. Ordinary Matter:
- Baryonic Matter: This includes all the matter we are familiar with, such as stars, planets, and living organisms. It makes up about 5% of the universe’s total energy density.
- Role: Ordinary matter forms galaxies, stars, and other cosmic structures. It interacts with light and other forms of radiation.
d. Radiation:
- Cosmic Microwave Background (CMB): Radiation from the early universe that provides a snapshot of the universe approximately 380,000 years after the Big Bang.
- Role: The CMB provides critical evidence for the ΛCDM model and helps determine parameters like the universe’s age, composition, and rate of expansion.
2. Key Features of the ΛCDM Model
a. Flat Universe:
- The model suggests that the universe is geometrically flat, which means that the total density of the universe is very close to the critical density. This is supported by observations of the CMB and the distribution of galaxies.
b. Evolution of the Universe:
- Early Universe: The ΛCDM model describes the universe’s evolution from a hot, dense state shortly after the Big Bang, through its expansion and cooling, leading to the formation of the first atoms, galaxies, and large-scale structures.
- Cosmic Inflation: The model incorporates the theory of cosmic inflation, a rapid expansion of the universe during its earliest moments, which explains the uniformity and isotropy observed in the CMB.
c. Structure Formation:
- The model explains how small density fluctuations in the early universe grew over time due to gravitational attraction, leading to the formation of galaxies and larger structures.
3. Observational Evidence
a. Cosmic Microwave Background (CMB):
- Measurements from the Planck satellite and other observatories have provided detailed maps of the CMB, supporting predictions of the ΛCDM model regarding the universe’s density and composition.
b. Supernovae Observations:
- Observations of Type Ia supernovae have shown that the expansion of the universe is accelerating, consistent with the ΛCDM model’s prediction of dark energy.
c. Large-Scale Structure Surveys:
- Surveys of galaxy distribution and clustering, such as those from the Sloan Digital Sky Survey (SDSS) and the Dark Energy Survey (DES), have provided empirical support for the ΛCDM model’s predictions about the distribution and behavior of cosmic structures.
d. Galaxy Clusters and Lensing:
- Observations of galaxy clusters and gravitational lensing effects have been used to map the distribution of dark matter and confirm the ΛCDM model’s predictions.
4. Current Research and Challenges
a. Hubble Tension:
- There is a discrepancy between measurements of the Hubble constant (the rate of expansion of the universe) obtained from local observations and those inferred from the CMB. This “Hubble tension” suggests potential areas for new physics or modifications to the ΛCDM model.
b. Dark Matter and Dark Energy:
- While the ΛCDM model effectively describes many aspects of the universe, the exact nature of dark matter and dark energy remains unknown. Ongoing research aims to understand these components better and refine the model.
Recent Research in ΛCDM Model
Refinements in Cosmological Parameters:
- Planck Satellite Data: The Planck mission, which provided detailed observations of the Cosmic Microwave Background (CMB), has refined estimates of several cosmological parameters. This includes the Hubble constant, the density of dark matter and dark energy, and the curvature of the universe. Planck’s results have been crucial in testing the ΛCDM model’s predictions.
- Update on Parameters: Recent analyses have provided updated values for the cosmological parameters. For example, the latest Planck data suggests a Hubble constant H0H_0H0 of approximately 67.4 km/s/Mpc, which is lower than some local measurements.
Large-Scale Structure Surveys:
- Dark Energy Survey (DES) and Vera C. Rubin Observatory: These surveys provide data on the distribution and behavior of galaxies, which helps in testing the ΛCDM model. DES and the upcoming Legacy Survey of Space and Time (LSST) at the Rubin Observatory aim to measure galaxy clustering, weak gravitational lensing, and the growth of cosmic structures to further test the model.
Hubble Tension Investigations:
- New Techniques: Researchers are exploring various methods to resolve the Hubble tension, such as refining local distance measurements, investigating possible systematic errors, and considering alternative models or modifications to ΛCDM that might reconcile the differences.
Modified Gravity Theories:
- f(R) Theories: These are modifications to General Relativity where the function of the Ricci scalar RRR is modified. They provide alternative explanations for accelerated expansion that could impact the ΛCDM model’s interpretation.
- Screening Mechanisms: These mechanisms, such as the Chameleon or Vainshtein mechanisms, attempt to explain why deviations from General Relativity are not observed in local environments but could affect cosmological scales.
Dark Matter Research:
- Direct Detection Experiments: Efforts are ongoing to detect dark matter particles directly through experiments like those at the Large Hadron Collider (LHC) or direct detection facilities such as XENON1T and LUX-ZEPLIN (LZ).
- Astrophysical Observations: Observations of galaxy rotation curves and cluster dynamics continue to provide insights into the properties of dark matter and its role in ΛCDM.
Mathematical Framework of ΛCDM Model
Friedmann Equations:
- The ΛCDM model is based on the Friedmann equations, which are derived from Einstein’s General Theory of Relativity. These equations describe how the universe’s expansion rate depends on its contents.
The Friedmann equation is
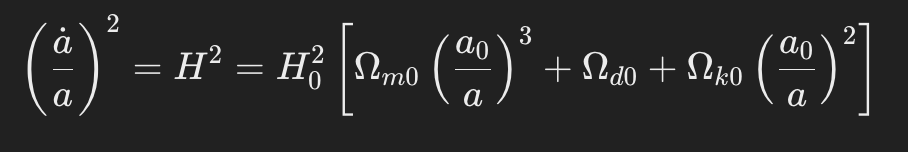
where:
- a is the scale factor at a given time, and a_0 is the scale factor at the current time. (it is usually set to 1)
- H is the Hubble parameter.
- H0 is the current value of the Hubble constant.
- Ωm0, Ωd0, and Ωk0 represent the current density parameters for matter, dark energy, and curvature, respectively.
Cosmic Microwave Background (CMB) Power Spectrum:
- The CMB power spectrum provides a detailed snapshot of the universe when it was just 380,000 years old. The ΛCDM model predicts the shape and amplitude of the CMB power spectrum, which has been confirmed by observations from the Planck satellite.
The angular power spectrum C_l is given by
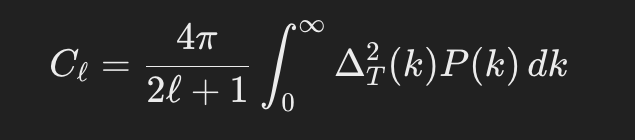
where:
- ΔT2(k) is the transfer function.
- P(k) is the primordial power spectrum.
Growth of Structure:
- The growth of cosmic structures is described by the linear growth factor D(a). This growth is influenced by the density of dark matter and dark energy.
The growth equation is:
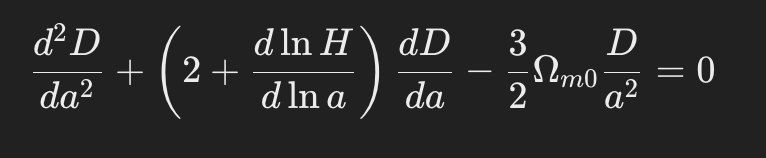
In summary, recent research on the ΛCDM model involves refining cosmological parameters, investigating the Hubble tension, and exploring modifications to the model. Mathematically, the ΛCDM model relies on the Friedmann equations, the CMB power spectrum, and the growth of cosmic structures to describe the universe’s evolution.
