Density Parameter ( Ω )
The density parameter is a dimensionless quantity used in cosmology to describe the ratio of the actual density of matter or energy in the universe to the critical density. The critical density is the density required for the universe to be flat, meaning that it has just enough mass and energy density to balance the expansion and prevent the universe from eventually collapsing or expanding too rapidly.
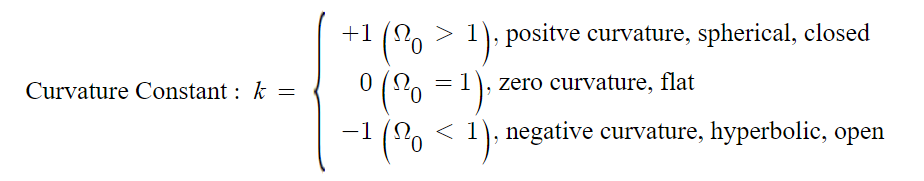
FLRW
The Friedmann-Lemaître-Robertson-Walker (FLRW) cosmological models are a set of solutions to Albert Einstein’s field equations of general relativity, describing the large-scale structure and evolution of the universe.
The FLRW models are based on the following key assumptions:
Homogeneity: The universe is assumed to be homogeneous, meaning that it looks the same at every point on large scales. In simpler terms, if you were to pick any two sufficiently distant regions in the universe, they would appear similar on average.
Isotropy: The universe is assumed to be isotropic, meaning that it looks the same in every direction on large scales. This assumption aligns with the idea that there is no preferred direction in the universe.
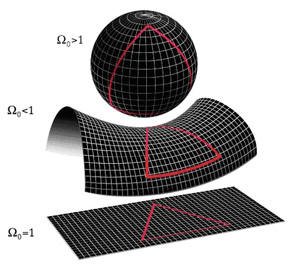
Spatial Curvature: The spatial geometry of the universe is described by its curvature. The possible spatial geometries include flat, open, and closed. The curvature is influenced by the distribution of matter and energy in the universe.
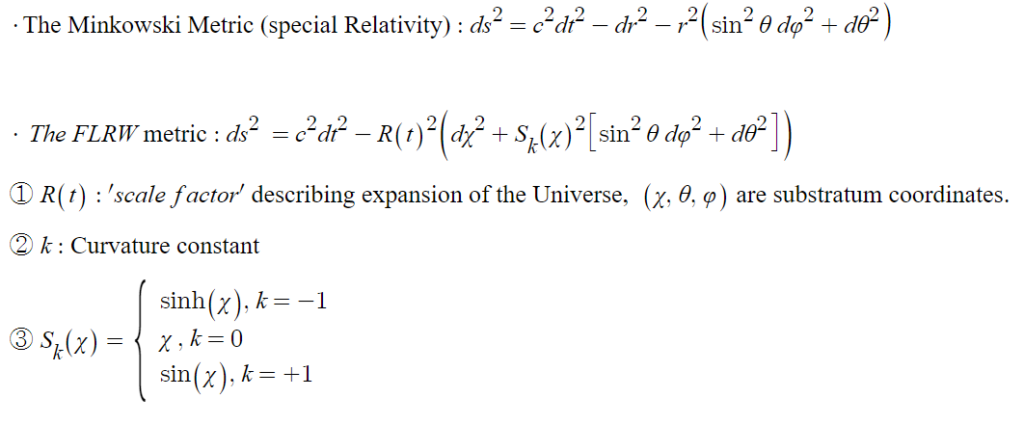
Friedmann Euqations
Using the FLRW metric, the Friedmann equations can be derived from the Einstein Field Equations of General Relativity.

Friedmann Models (Λ = 0, p=0, ρ >0 )

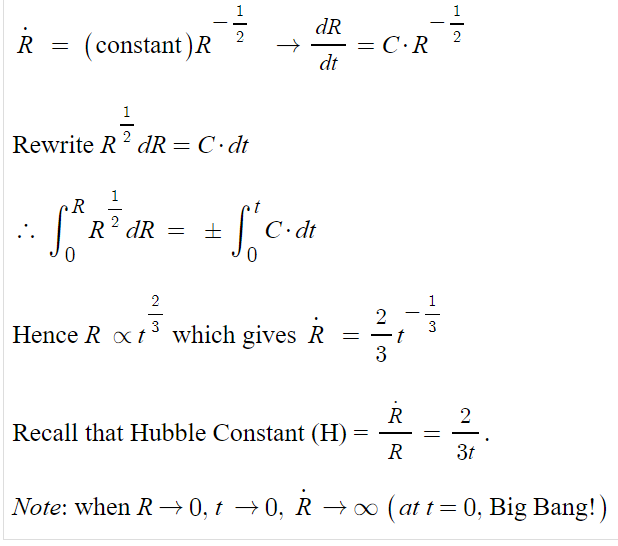
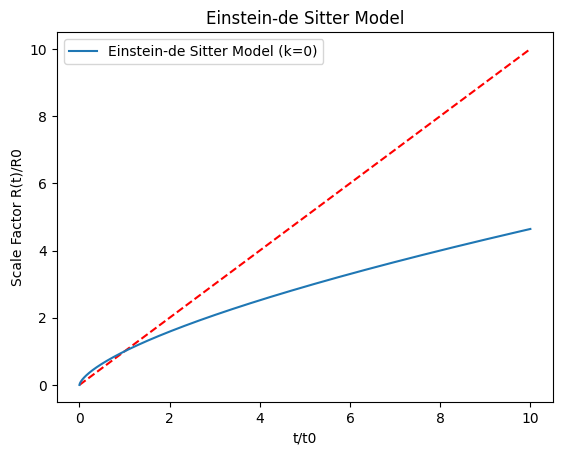
Einstein-de Sitter model
The Einstein-de Sitter Model, characterized by a flat spatial geometry (k=0), serves as the boundary between cosmological models with positive curvature (closed) and negative curvature (open). In this model, the universe is matter-dominated, meaning that the density of matter is precisely at the critical density needed for a flat universe.
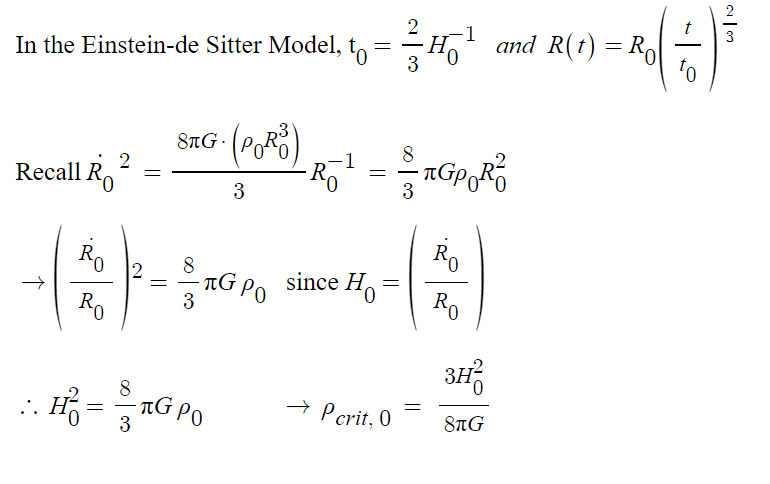
The critical density (p_crit) is the density required for the universe to be spatially flat, where the geometry is neither positively curved (closed) nor negatively curved (open). The density parameter is defined as:
Ω= p_0 / p_crit, where p_0 is the actual density of the component (e.g., matter, radiation, dark energy) in the universe.
Using Python, we can visualize how the Einstein-de Sitter model looks.